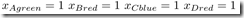Applications of Graph Theory
Graph Theory is just a beautiful part of mathematics. Not only Computer Science is heavily based on Graph Theory. There are a lot of applications of Graph Theory in Operational Research, Combinatorial Optimization, Bioinformatics. For my personal clasification I have separated the tasks, which you can solve using Graph Theory into two groups:
- Obvious applications – I mean, that the analogy between the
graph and the problem is quite easy to imagine (maps, cities,
relations etc.). In this post you can find the following:
- Vehicle Routing Problem
- Graph coloring
- Map coloring
- Hidden applications - Tasks which you would never assume can be
solved using Graph Theory. Than you see one of them, and than you
think: “Wow, I wonder who came up with that one…”. I will provide
the following ones in this post:
- Image or 3D model reconstruction from projections
- Prove of NP hardness of Integer Linear Programming
- Register allocation
- Approximation of data, data compression
- Task scheduling
Obvious applications
Here are some examples of problems for which the creation of the graph to model the problem is quite easy and obvious.
Vehicle routing problem and other variants of TSP
There is a whole set of problems, which are just variations of Traveling Salesman Problem. Vehicle Routing Problem (VRP) can be characterized by following description:
- We are provided with a set of trucks, each of a certain capacity
- Set of customers, each with certain need of the goods
- The central repository, where the goods are stored
The tasks is to root the trucks, to distribute the goods to the clients and minimalize the distance. I have written a blog and a web utility which is able to solve the problem using two algorithms:
- Clark & Wright Savings Algorithm
- The Sweep Algorithm
You can find more algorithms for solving VRP here.
Graph coloring problem
Given a graph, we want to decide, whether it is possible to color each of the vertices in the graph in such way, that none of the vertices which are sharing and edge have the same color. Many real world problems can be formulated as Graph coloring problem. Ne first one of the Map coloring.
Map coloring
One of the first application is the map coloring problem. It has been proven, that each map can be colored using 4 colors. This problem can be converted to graph coloring problem by placing the vertex inside each country or region in the map. Two vertices are connected if and only if the two countries have a common border. More over here.
Hidden applications
There are tasks and problems for which you would not intuitively search the solution by applying graph theory. Here are some of them:
Image reconstruction from X-Rays – Computer tomography.
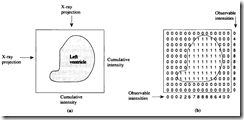
Tomography is a technique used to reconstruct an image or 3D model from series of projections, subsequently taken from different angles. When using technologies such as the x-rays, the image take from an angle gives for each pixel the total thickness of the scanned object. The questions is than how to reconstruct the image from several taken images which are containing only the thicknesses.
As described in great book “Network Flows – Theory, Algorithms and Applications”, concrete example of computer tomography is the “Reconstruction of the Left Ventricle from x-Rays projections”. This problem can be solved using the application of network flows theory. This method is applicable only to problems where the scanned object has a uniform structure. As mentioned in the book this assumes that the well-working Ventricle is filled uniformly with blood and dye mixture.
The following graphics was taken from the book. It explains the method on two dimensional image. Using two projections of the project, we obtain vectors which are containing for each pixel (or other unit) the probable mass hidden behind this pixel. Now is up to us to find out how this mass is distributed - that means where are the ‘1’ in the picture. The more projections we have, the better results we can obtain.
The problems is thus simplified to the problem of constructing binary matrix from the projection sums. This problem is a special case of the feasible flow problem.
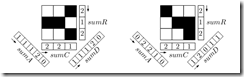
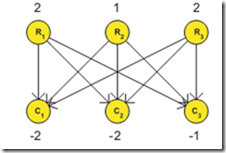
The following image shows similar very simplified task, which I have taken from the Combinatorial Optimization course offered as part of Open Informatics program at CTU Prague.
The whole problem can be seen as the question of finding the feasible flow in a network (G, b, u, l,c). So what does network consist of:
- Graph G
- s – sources – the nodes which provide the fluid into the network – the nodes with positive values
- t – appliances (or sinks) – the nodes which consume the fluid – the nodes with negative values
- u – upper bound for the flow of each edge
- l – lower bound for the flow of each edge
- c – the actual flow in each edge – the one for which we are looking. The task is to find the values of c for each edge, in order to satisfy all sinks.
Here is the graph G which corresponds to the projections sumR and sumC from the previous image. Each edge in the graph corresponds to one pixel, connecting the two projections. The sumR are being sources in this network and the sumC edges are sinks.
For each edge the lower bound l(e) = 0, upper bound u(e) = 1 and we are looking for values of values of c(e), in order to for the flow to be feasible and also minimal. The edges which are used in the feasible and minimal flow are pixels which will have ‘1’ value in them.
Proving NP’s ness of some problems such as Integer Linear Programming
The graph coloring problem has been already mentioned above. We are trying to color each node of the graph in such a way, that nodes with same color cannot be connected by an edge.
Integer Linear Programming (ILP) is NP-hard problem. This can be proven by the polynomial reduction of Graph coloring problem to the ILP problem. Concretely we can say, that for each graph which can be colored using 3 colors, we are able to construct an ILP problem, which has a solution. From the theoretical point of view saying “we are able to construct” means that there is a polynomial reduction of Graph coloring problem to ILP problem. Polynomial reduction proves that:
- If Graph Coloring is NP-hard problem, than ILP is also NP hard problem.
Polynomial reduction has to satisfy two conditions in order to prove the NP-hardness:
- The reduction algorithm – the construction of one problem from another has to be performed in polynomial time
- For each instance graph which can be colored with 3 colors an instance of ILP can be constructed which has a solution
Here is the reduction algorithm (the algorithm which explains how to define an ILP problem to given graph):
In the beginning we have a graph colored using 3 colors. We will try to create an instance of ILP out of this graph. That means we have to define the variables and the equations which build the ILP problem. We can do this in 3 steps.
- Create N variables x~ncolor~ == 1 <=> the node n has the color c, where N is the number of nodes.
- For each node in the graph add en equation to the ILP system:
- x~nred~ + x~nblue~ + n~ngreen~ = 1
- for each edge e = {n~i~, n~j~} in the graph add following three
equations in the system:
- x~nired~ + x~njred~ <= 1
- x~niblue~ + x~njblue~ <= 1
- x~nigreen~ + x~njgreen~ <= 1
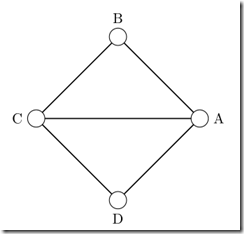
Here is an example, we have an simple graph:
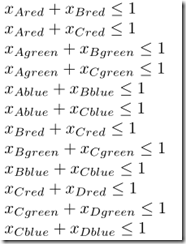
Now the first set of equations, which states, that each edge can have at most one color:
The following set of equations, which states, that nodes sharing edge cannot have the same color:
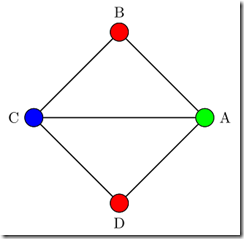
Now because the ILP problem can be reduced to graph coloring problem, we know, that this problem has solution, when the graph can be colored with three colors. Here is the solution:
Which corresponds to:
The coloring of the graph is NP hard, so also ILP is NP hard. If you wonder how to prove that NP graph coloring is NP hard: there is a polynomial reduction from one special type of SAT problem.
Register allocation
Register allocation is the process of assigning possibly infinite set of variables of assembly program to a finite set of registers which are available in the processor. Not all variables are used at the same time, so several variables can share a register (if not this mapping would not be possible). Even this problem is solved using graph coloring. For each variable a vertex is created. Vertices are connected if variables “live” in the program at the same time. The number of colors given to color the graph is equal to number of registers.
Approximation of the data – data compression
This technique is used in order to approximate the data which has to be stored while minimizing the loses of precision.
For example a data which represents taken temperatures during the time and builds a nice graph. However if this data was taken at high frequency, there might be too many records. The idea is to minimize the number of records, while keeping most of the information about the evolvement of the temperature.
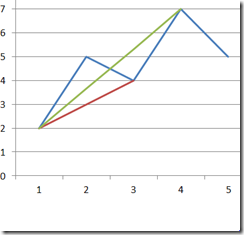
The shortest path algorithm can be used to solve this problem. For instance the blue line in the following graphics represents the data to be stored. It is 10 values: the time x and Temperature( x) at the time x. The green and red line represent possible approximations, when we are leaving out one or two nodes. Of course there are several nodes which can be left out and the shortest path algorithm can help us to find which ones can be left out.
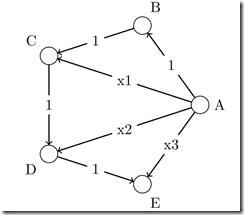
We can construct a full graph, which will contain 5 nodes, representing the 5 data points (the times x). Each edge represents the “precision loose” which we pay, when we take the direct path between the two nodes of the edge instead of passing the traditional way. The following picture represents the partial graph – the skipping edges start only in the first node ( A ). The edge with value x1 corresponds to the red line in the graph etc. The graph should be also filled with other edges starting in B and C (the only edge going from D to E is already present and there are no edges starting in E), but I have left them out for simplicity.
So without compression we have the simple path: A,B,C,D,E = 1 + 1 + 1 + 1 = 4
Taking the red edge and the rest of the path: A,C,D,E = 1 + 1 + 1+ x1
Taking the green edge and the rest of the path: A, D, E = 1 + 1 + x2
The values of the edges in the standard path should be the lowest (here all of them have value 1). On the other hand values of edges which will make us loose more precision should be the greatest. Then of course we can introduce some bonus to motivate the algorithm to take less edges (better compression). All this constraints can be modeled using heuristics.
One possible heuristics to evaluate the value of the edge is to measure the distance between the real data and the estimated date. For instance the value of the second point is 5. If we estimate the value using the red line (leaving out the second point) the corresponding value on the red line is 3. The distance between these two values is: 2.
If we use the the green line instead then the distance between the estimated value f’( x) and the real value f( x) is 1. On the other hand the green line also estimates the second point 3 point. And we see that the distance for the second point will be more or less 1.5. So we should add these distance together. So we get:
x1 = 2
x2 = 2.5
This is just a proposition. We could also multiply it by some coefficient to obtain some reasonable results.
With the developed and evaluated graph, finding the shortest path in the full graph from the node A to the node E will give us the best “size/precision” ratio.
Task scheduling
In this problem we have a group of workers and group of tasks. Each task can be processed by each worker. However the workers do not have the same performance on all tasks – the time for the processing of each task differs for each worker.
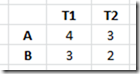
Let’s take a look at very simple example, we have two workers (A,B) and two tasks (T1,T2). The values in the table represent the processing time, that the worker needs for the given task.
This can be solved as finding the cheapest flow in the following graph.
Not that each edge has two values: u/c. The ‘u’ represents the capacity of the edge – it is always one. The ‘c’ represents the cost of the edge. Finding the cheapest flow in this graph from S to F will give us the best assignment of workers to tasks.
Other interesting applications
- Development of custom processors for minimization of resources – data path optimization.
- Scheduling on parallel processors – application of maximal flow finding problem.